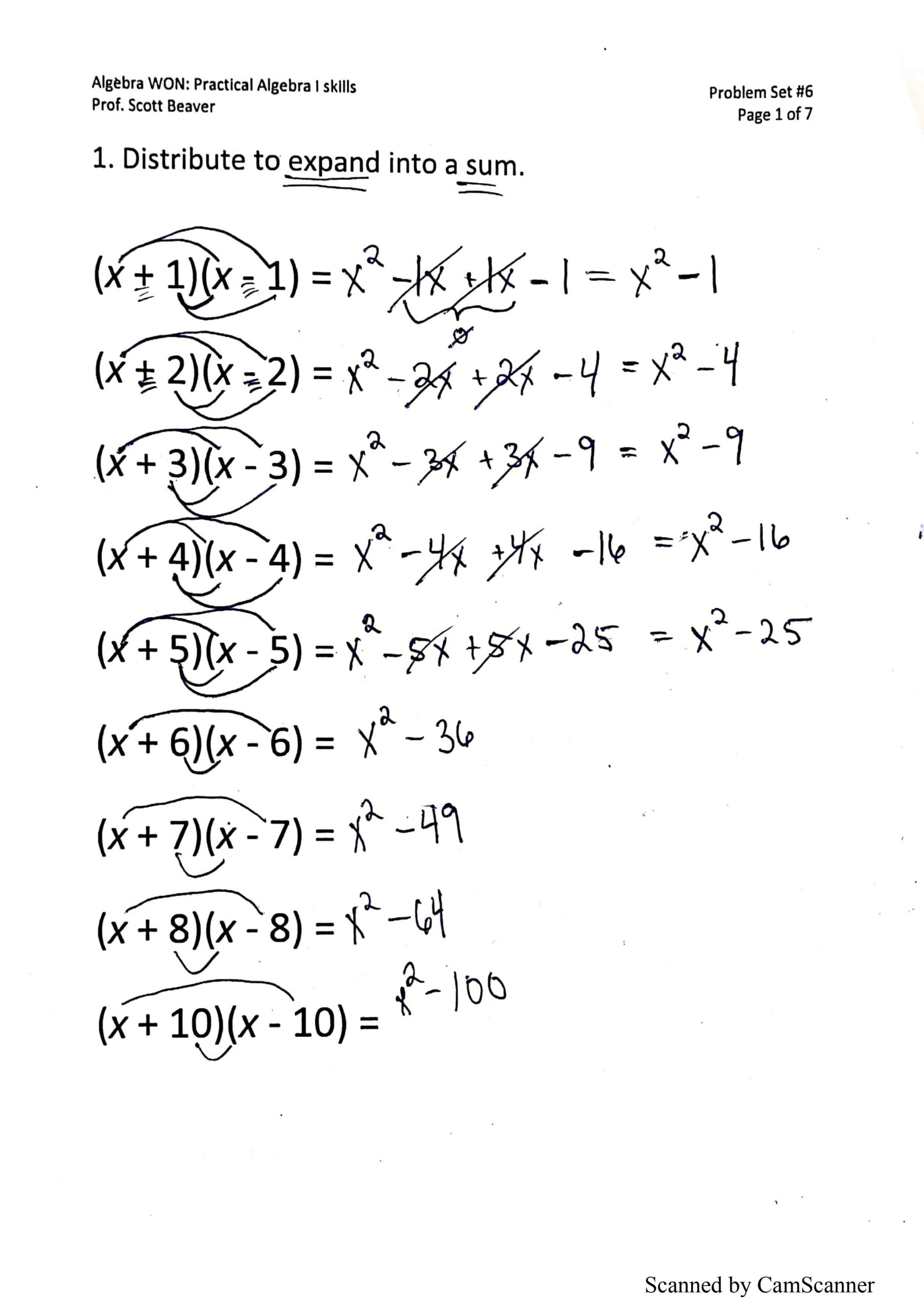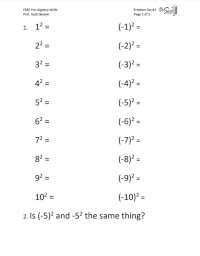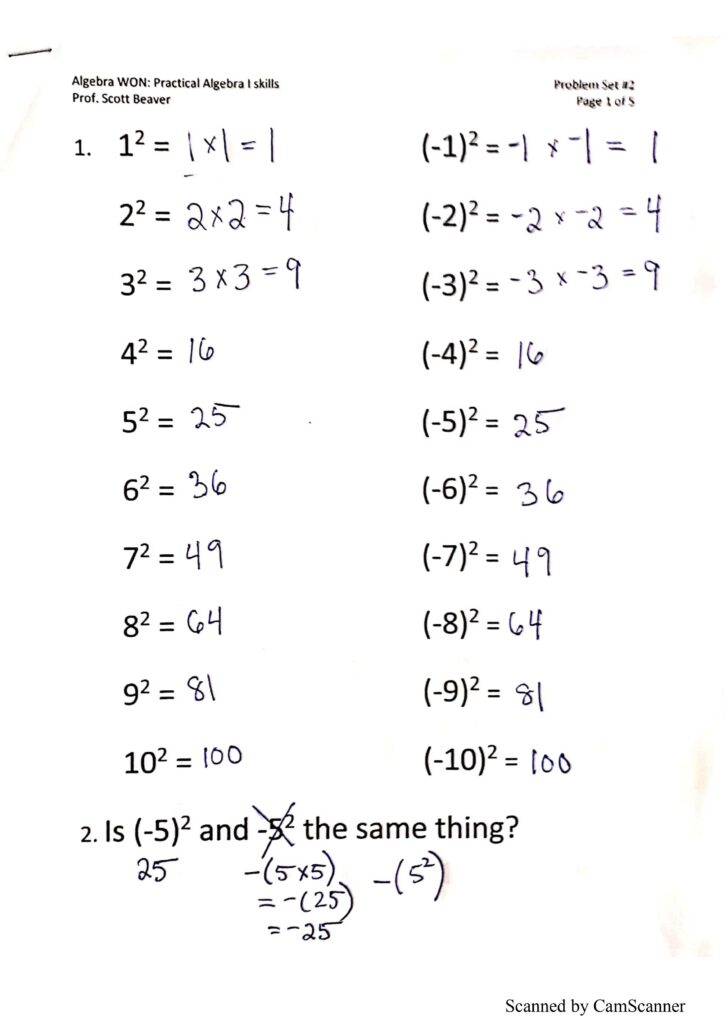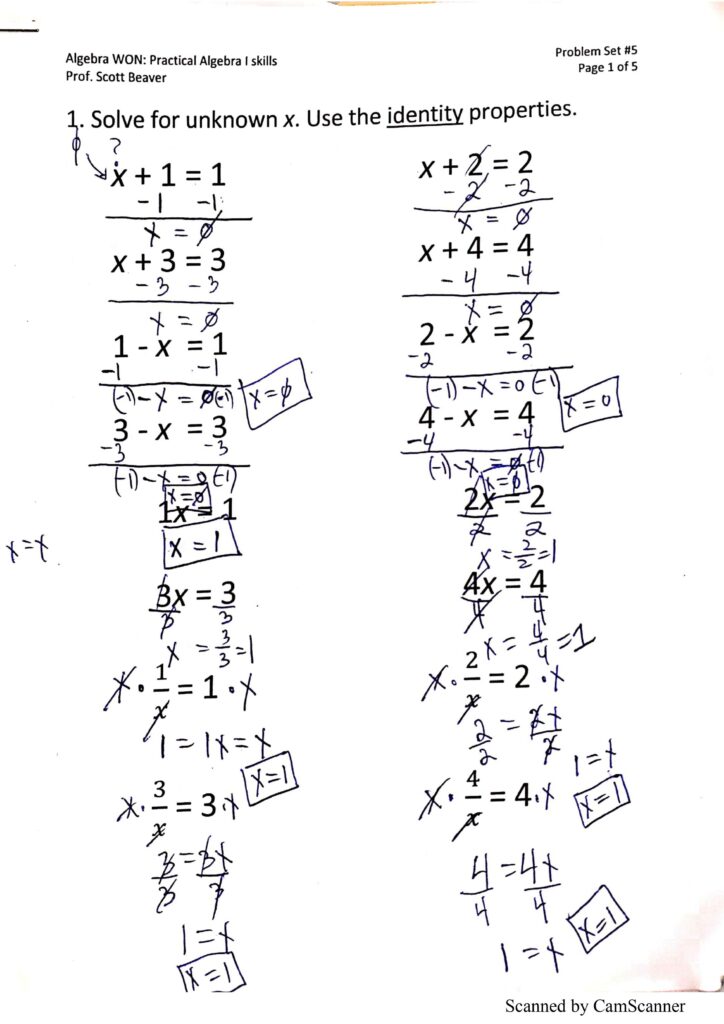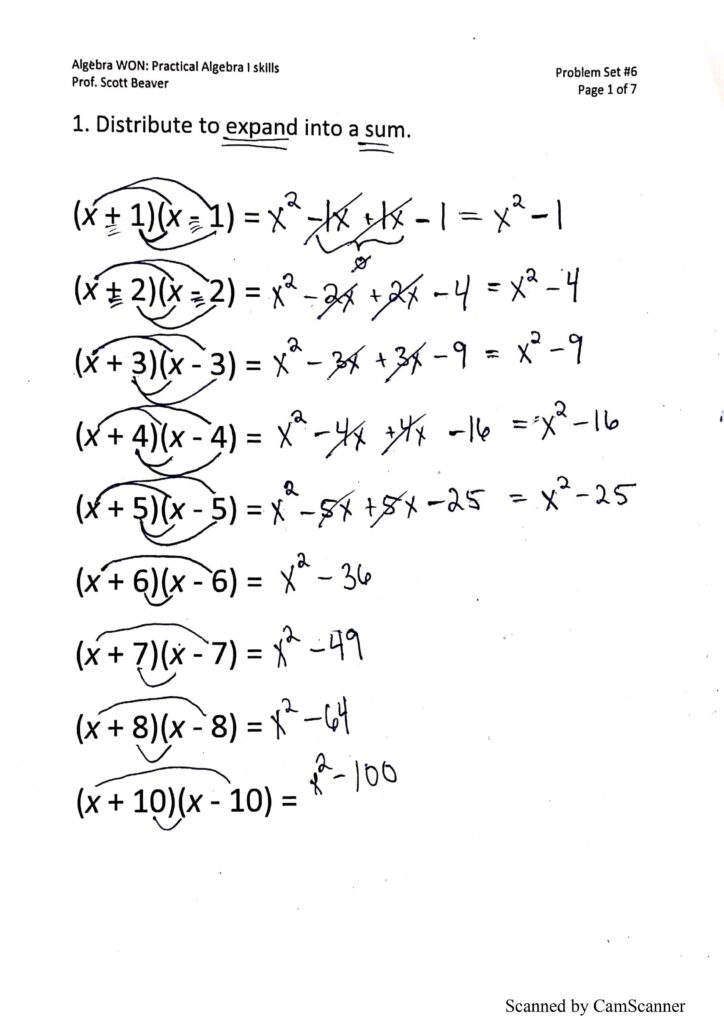Algebra 1 Worksheets with Answers PDFs
About our Algebra 1 Worksheets with Answers
Our Algebra 1 worksheets with answers in pdf format are designed to show you the patterns of math, the easy way. There’s a video course showing all the steps for all the algebra 1 problems found in the worksheets, or you can purchase the answer keys for the free algebra 1 worksheets found below.
Learn algebra 1 fast, in a fraction of the time of a normal class.
Focus only on the important algebra 1 concepts.
Master easy algebra problems using the numbers zero through nine.
What the Algebra 1 Worksheets Cover
Download our Algebra 1 Worksheets
Download the printer-friendly worksheets below, and also find the complete video solutions and lessons here.
Problem Sets 1, 2, 3 and 4 cover the topics needed for algebra 1 success, including order of operations, distributing, scientific numbers, and cross multiplication.
The algebra 1 worksheets answers are found at the bottom of this page.
Problem Set 5: Finally Some Algebra
PS5 focuses on solving equations involving a single variable x. It’s a rather lengthy worksheet covering the many, many common types of equations containing the variable x. You will learn how to systematically apply inverse operations to isolate the variable x algebraically. We commonly call these techniques simply solving an equation by hand, using paper and pencil.
Problem Set 6: Factoring Perfect Squares
PS6 covers an extremely specific technique known as factoring a difference of perfect squares. It’s a special case, yet we cover it extensively because it leads naturally to the factoring of more general types of expressions. Factoring, which is conceptually the opposite of a distributing, is probably the single most important all the algebra 1 topics.
Problem Set 7: Factoring Expressions
PS7 covers the topic of factoring for the general case of polynomial expressions. This is an important technique that will allow us to solve equations.
Problem Set 8: Factoring Equations
Problem Set 9: The Quadratic Equation
Algebra 1 Worksheets Answers PDFs
Download the partial algebra 1 worksheet answer key pdfs by clicking on the images.
Click to purchase the complete answer key pdfs to the above algebra 1 worksheets, including all the answer key pages.
Purchase the Complete Algebra 1 Course Materials
Instantly unlock the COMPLETE answer keys (all pages) for the 9 problem sets for just $15, in pdf format similar to above.

Get ALL the explainer videos plus the answer keys (all pages) for the 9 problem sets. Certificate of completion included.