About the Significant Figures Worksheet
The Significant Figures Worksheet covers sig figs, as they say, a topic found in chemistry classes that doesn’t exactly look like chemistry.
In Plain English, significant figures are used for rounding numbers. Rounding is a simple concept we usually learn in elementary school. We all know how to round: 0-4 round down, and 5-9 rounds up. Sig figs are used to determine where we should round. That is, should your final answer have 3 decimal places? Or none? How precise should your answer really be? Significant figures are used to express the idea of precision in science.
We have clear examples below that show you 3 simple rules to apply sig figs correctly in every situation. Sig figs is a fairly easy concept (really!) that usually looks difficult because it’s usually taught poorly. Again, we are just talking about rounding numbers. Everybody knows how to round, and sig figs tell us how many digits to round to.
You’ll also find the significant figures worksheet at the bottom of the page to get sig fig practice and master the topic.
Download the Significant Figures Worksheet
Download and print the black and white pdf. It’s 2 printer-friendly pages. Click here for the answer key.
Sig Figs: Who cares?
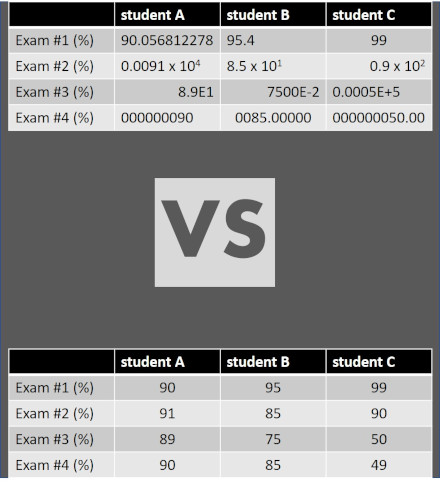
Take a look at the data in the below image. There are 4 grades for 3 students A, B, and C. Does the data block above look horrible and disorganized? It’s the same data as the bottom half of the image, where you can clearly read the numbers.
Why is the bottom version better? Because the numbers are all lined up! An accountant would line up the decimals between the dollars and cents. When a scientist organizes data, sig figs are used to neatly line up the data. In other words, sig figs simply prevent ugly looking data from ruining your otherwise beautiful analysis. If you don’t want ugly data, you need to master sig figs. (Plus you’ll get more points in chemistry class and lab.)
Significant Figures Rules
What is a Significant Figure?
There are 3 simple significant figures rules. Generally, any digit 1-9 counts as being significant, but zeros (0’s) may or may not be significant. When we look at a number, we can count the number of digits that are significant.
Plus you need to know adding significant figures and sig figs for multiplication. There is a Significant Figures Worksheet at the bottom to get your sig figs practice!!!
Sig Fig Rules #1
Leading Zeros never count.
Leading Zeros never count. Leading zeros mean any zeros on the LEFT side of a number.
For example, sometimes an odometer on a car reads something like 050429 km. That leftmost zero, the leading zero, is meaningless. It’s just a place holder. The number is the same as 50429, better with a comma as 50,429. There are 5 significant figures here.
Leading zeros can also happen with a decimal point! For example, 0.00000000012 has just two significant figures. Just the 12 at the right of the number are significant digits. None of the leading zeros, ten of them in this case, are significant digits.
In summary, leading zeros never count as significant digits. It doesn’t matter whether there is a decimal point or not. Leading zeros never count. Period.
Sig Fig Rules #2
Trailing Zeros Count, if there's a decimal point.
Trailing Zeros Count, if there’s a decimal point.
Sig Fig Rules #2 is a bit different than Sig Figs Rules #1. Now there are two different cases, depending if there is a decimal point or not.
The number 39.00 has a decimal point. Therefore the trailing zeros count as significant digits. There are four significant figures in 39.00.
The number 3,900 does not have a decimal point. Therefore the trailing zeros do NOT count as significant digits. There are two significant figures in 3,900.
Sig Fig Rules #3
Middle Zeros always count.
Middle Zeros always count.
This rule is pretty simple. All digits 0-9 count in the middle of a number.
For example, 1,000,001 (a million and one) has 7 significant figures. They all count, as all the zeros are in the middle. Compare that to 1,000,000 (a million, with 6 trailing zeros and no decimal) which would have just 1 significant figure.
From above, the number 50,429 has 5 significant digits. There is a zero, in the middle, so it’s just treated like any other digit. They all count as significant digits in 50,429.
Sig Figs Multiplication
For sig figs multiplication, go with the fewest significant figures.
Consider 11.1 with 3 significant figures multiplied by 22.22 with 4 significant figures. That’s 11.1 times 22.22. In a calculator, the answer would be 246.642. But we only want to keep 3 significant figures after rounding, since 11.1 only had 3 significant figures. So the final answer would be 247 after rounding to the nearest whole number to ensure there are exactly 3 significant figures. The calculator answer of 246.642 is “wrong” because it is too precise.
The same general idea applies to division as well.
Adding Significant Figures
When adding significant figures, go with the fewest decimal places. (The significant figures don't actually matter.)
Consider 11.1 with 1 decimal place added to 22.22 with 2 decimal places. That’s 11.1 + 22.22. In a calculator, the answer would be 33.32. But we only want to keep 1 decimal place after rounding, since 11.1 only had 1 decimal place. So the final answer would be 33.3 after rounding. The calculator answer of 33.32 is “wrong” because of the funny, inconsistent “2” at the end which doesn’t “line up” properly with other digits, which are all 3’s.
The same general idea applies to subtraction as well.
Sig Figs Multiplication and Addition Combined
Keep track of the sig figs at each step of a multistep calculation. Round only at the end.
Consider a calculation like (3.5 – 3.0)/3.0 or in general (A-B)/B where A and B could be any number. This is an extremely common case in a chemistry class for calculating things like percent change and percent error. If you don’t learn this, you are going to lose points on your percent error calculations in lab reports… that’s a lot of points to lose!
Let’s do (3.5 – 3.0)/3.0 to get an answer. First thing, the rules of algebra say to do the subtraction first, then the division. So take 3.5 – 3.0 and you get an intermediate answer of 0.5. That’s a leading zero (never counts), only the 5 is a significant digit, and there is just 1 significant figure total in 0.5.
Next we divide 0.5 (1 sig fig) by 3.0 (2 sig figs). Get a calculator. It would say 0.1666666….. That’s a zero, a decimal point, a one, and a repeating six. We should round to 1 significant figure, since 0.5 had just 1 sig fig. (Note the rule for division and multiplication is the same, to go with the fewest sig figs.) So the final, rounded answer would be 0.2 to have exactly 1 sig fig (the leading zero never counts).
Now, you might think that since (3.5 – 3.0)/3.0 has three numbers all with 2 sig figs, the final answer would also have 2 sig figs. Wrong. That’s not how the rules work. You have to go through the steps and track the sig figs. For the record, the (A-B)/B type of calculation is specifically designed to destroy sig figs… those poor, poor destroyed sig figs… so that calculated percentages don’t end up unreasonably precise and therefore dubiously cloud your lab result. Destroying sig figs is a good thing, and be sure to do it when you see this type of calculation!
Is There More?
If you really want to learn significant figures really well, you should understand scientific numbers. There is a worksheet and lesson here in our Pre-Algebra course. The topics will make more sense when you know them both.
Significant figures is a subtopic of the larger topic of error analysis, which requires some more math skills. Fortunately sig figs are easy, since we are just talking about how to round numbers.